주요 참고자료

MASTER THESIS no. 1375 Physically based rendering, Jure Ratkovic, Zagreb, April 2017

Unreal 물리 기반 머티리얼

PBR 이란 무엇인가?(그냥 그런 블로그)

PBR(Physically based rendering)이란?

Light, Unreal 물리 기반 머티리얼

물리기반 렌더링(Physically based rendering, PBR)은 이름과는 반대로 표면이 현실의 라이트 작용 방식을 모방한다는 뜻입니다. PBR 원칙에 부합하는 머티리얼은 아티스트의 직관에만 의존하여 파라미터를 세팅하는 셰이딩 워크플로보다 더 정확하고 자연스럽게 보입니다. PBR은 최고레벨의 현실성과 정확한 빛 모델과 물질간의 상호작용을 통하여 최고 레벨의 렌더링 퀄리티를 시도하도록 쉐이딩 모델을 둡니다. PBR의 쉐이딩 공식들은 빛의 상호작용 법칙들로 부터 도출됩니다. 물리학적 개념들, 확산, 반사 그리고 에너지 보존등은 엄격한 수학적 프레임워크, 물리학적으로 정확한 쉐이딩 공식을 제공하기 위한)아래서 연구됩니다.

이전의 쉐이딩 모델, Phong, Blinn-Phong등은 속임수입니다. 이들은 다양한 라이팅 조건 밑의 관찰되는 오브젝트나 유사한 결과를 내도록 발명한 쉐이딩 공식들 입니다.

graph RL MeasureOfLight--->Light LightAttenuation--->MeasureOfLight LightAttenuation--->Light PhysicsOfLight--->Light Radiometry&Photometry--->MeasureOfLight Illuminance&Luminance--->Radiometry&Photometry Absorbed--->PhysicsOfLight Transmittance--->PhysicsOfLight Scattering--->PhysicsOfLight FresnelEquation--->Cook-TorranceSpecularBRDF NormalDistributionTerm--->Cook-TorranceSpecularBRDF GeometricTerm--->Cook-TorranceSpecularBRDF Cook-TorranceSpecularBRDF--->BRDF LambertsDiffuseBRDF--->BRDF BRDF--->Reflection Reflection--->FresnelRaw Reflaction--->FresnelRaw FresnelRaw--->Scattering

물리기반 머티리얼은 모든 라이팅 환경에서 동일하게 잘 작동합니다 또한 머티리얼 값이 덜 복잡해지고 상호 의존성도 줄어들기 때문에 머티리얼 제작 워크플로가 더 사용자 친화적입니다. 이러한 장점은 픽사나 디즈니의 영화처럼 포토리얼하지 않은 레더링에도 적용됩니다. 최근 몇년간, 그래픽 처리 수용량의 증가로, 물리기반 렌더링은, 실시간 처리 제품(게임 같은 것들)에 폭넓게 적용되었습니다. 이러한 산업의 관심사로 인해, PBR 필드의 개발은 매우 빠릅니다.

PBR과 블림 퐁 모델의 퍼포먼스 차이는(쉐이딩 모델들에 대해서) 현대의 GPU에서 무시할 수 있습니다.
PBR의 단점은(drawbacks) 높은 스타일라이즈 그래픽에 대한 상대적으로(relatively) 낮은 적용 가능성입니다. (비록 최근에 많은 게임들이 PBR과 함게 스타일라이즈된 그래픽을 성공적으로 사용했습니다.)
PBR에 비해 BlinnPhong의 작은 성능 우위는 매우 제한된 하드웨어 환경(모바일 플랫폼 같은데)에서 고려될 수 있습니다.

graph LR SubsurfaceScattering--굴절되어 다시 나오는 빛-->Refraction Roughness--미세 융기로 인한 거칠기-->Reflection Specular--->SubsurfaceScattering Reflection--->Scattering Refraction--->Scattering Scattering--->PhysicsOfLight

빛의 측정(Measure Of Light)

방사측정(Radiometry)과 광도측정(Photometry)

Radiometry, Photometry

에너지가 입자나 파동의 형태로 전달되거나 방출되는 것을 방사선(radiation)이라고 합니다. 즉 가시광선을 포함한 전체 파장 영역의 전자기파들로 구성된 빛을 방사선이라 부를 수 있는 것입니다.

넓은 의미에서(전체영역) 빛을 다루기 위해서 에너지를 측정하는 것을 방사측정(radiometry)이라 합니다. 그리고 좁은 의미에서(가시영역) 빛을 다루기 위해서 에너지를 측정하는 것을 광도측정(photometry)이라고 합니다.

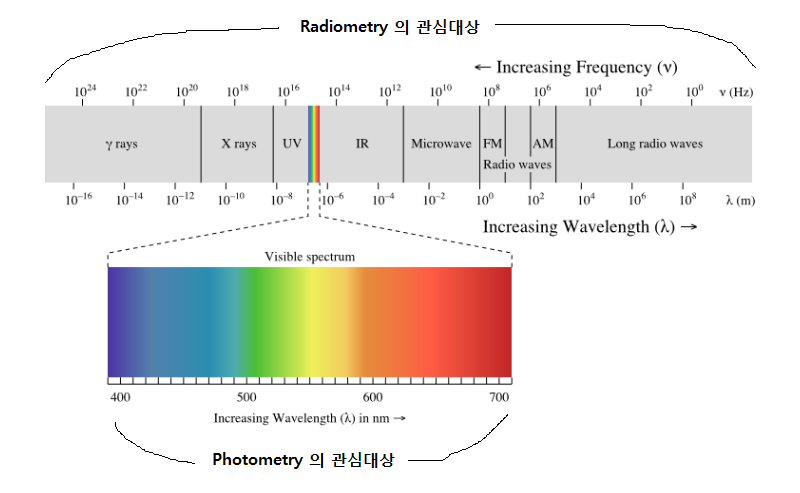
IlluminanceaAndLuminance

방사측정에서는 제곱미터당 일률(watt per squre meter)의 단위로 에너지를 측정하고, 광도측정에서는 제곱미터당 루멘(lumens per squre meter, lux) 단위로 에너지를 측정합니다.

radiance, irradiance는 방사측정에서 사용하는 용어이고, luminance, illuminance는 광도측정에서 사용하는 용어입니다. 단지 어떤 영역의 파장들을 다루고 있느냐, 에너지를 어떤 관점에서 바라보느냐의 차이가 있습니다. 그러므로 일반적으로 그래픽스에서는 radiance를 luminance로 irradiance를 illuminance로 대체해서 이해하셔도 무방합니다. 그래픽스에서는 빛을 photometry의 관점에서 다루고 있기 때문에 큰 차이는 없습니다

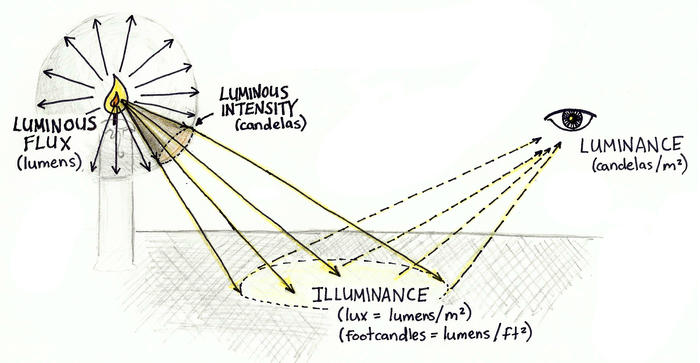
조도(Illuminance)와 휘도(Luminance)

Illuminance, Luminance

Luminance는 Photometric에서 주어진 방향으로 이동하는 빛의 단위 면적당 광도의 광도 측정입니다.

휘도는 종종 평평한 확산 표면에서 방출 또는 반사를 특성화하는 데 사용됩니다. 휘도 레벨은 특정 시야각 에서 특정 표면을 바라보는 육안으로 얼마나 많은 광도 를 감지할 수 있는지를 나타냅니다. 따라서 휘도는 표면이 얼마나 밝게 나타날 것인지를 나타내는 지표입니다.

Photometry에서 Illuminance는 단위 면적당 표면에 입사되는 총 luminous flux입니다. 입사광 이 표면을 비추는 정도를 측정한 것으로, 인간의 밝기 인지와 상관 관계가 있는 광도 함수 에 의해 파장 가중됩니다.

조도는 이전에 종종 밝기 라고 불렸지만 이것은 휘도 를 의미하는 것과 같이 단어의 다른 용도와 혼동을 일으킵니다. “밝기”는 정량적 설명에 사용되어서는 안 되며 생리적 감각과 빛의 인식에 대한 비정량적 언급에만 사용됩니다.

IlluminanceaAndLuminance

빛의 감쇠(Light Attenuation)

Light Attenuation

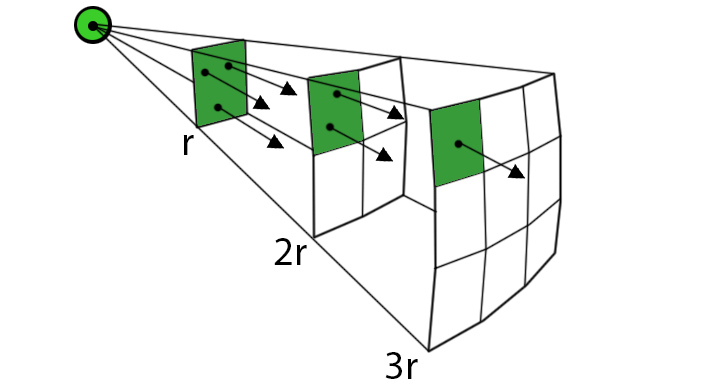
IlluminanceaAndLuminance

역제곱 법칙(Inverse square law) : 화살표는 소스에서 나오는 플럭스를 나타냅니다. 단위 면적당 화살표의 밀도(녹색 사각형, 밀도 플럭스)는 거리의 제곱에 따라 감소합니다.

\[Intensity = \frac{1}{distance^2}\]

물리적으로 올바른 감쇠의 주요 문제는 0에 도달하려면 영원히 걸린다는 점과, 디퍼드 라이트닝에서 아주 적은 이득을 위해 많은 픽셀을 처리한다는 단점이 있습니다. 이를 해결하기 위한 방법으로 falloff를 적용시키는 것 입니다.

\[(Unreal4)\ E=\frac{saturate(1-(distance/lightRadius)^4)^2}{distance^2+1}\]

빛의 물리학(Physics of light)

빛은 전자기적 횡파입니다. 물질의 전자기적 특성의 차이에 따라 다른 상호작용을 합니다. 상호작용을 정의하는 물리적 특성은 굴절률(reflactive index)입니다. 이 지수는 복잡한 숫자입니다. 물질 안에서 빛의 속도를 결정하는 진정한 부분인, 그리고 파장을 얼만큼 흡수하닌지 결정하는 복잡한 부분입니다.

표면(surface)에 도달한 빛이 모두 관찰자의 눈으로 들어 오는 것은 아닙니다. 어떤 매질(재질)의 표면에 입사한(incident) 빛은 흡수(absorbed)되거나 투과(tramsmitted)거나 반사(reflected)됩니다. 우리는 어떤 물체에서 반사된 빛만을 인지할 수 있습니다.

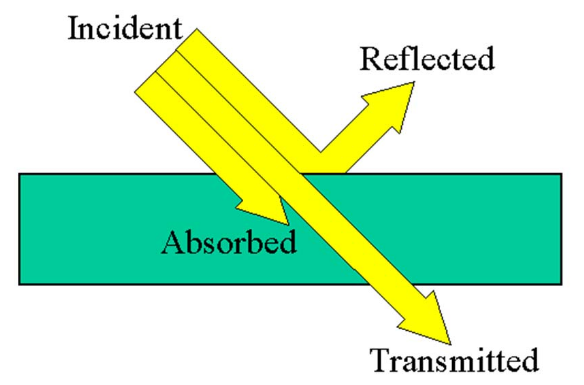
Waves

라이트 머테리얼을 결정하는 간단한 형태는 빛이 균질메체를 통과하는 것 입니다. 균등한 굴절률을 갖는 매개의 체적을 통과를 예로 들 수 있습니다. 지수의 복소수 부분이 낮으면(If the complex part of the index is low), 매개(media)는 투명한 것 처럼 보입니다. 그리고 높다면 매개는 특정 길이의 빛을 흡수합니다. 이로인해 색깔을 가지게 됩니다. 이러한 light material의 상호작용을 absortion이라 부릅니다.

매질이 이질적(heterogeneous)일때 굴절률이 갑자기 작은 길이(over small distance)에서 변경되면, 빛은 매질에 부딪혀 scatters 됩니다. 가능한 모든 방향으로 말입니다. 빛의 분포는 가끔식 정규화 되지 않습니다. 대신 특정 방향으로 spike합니다.표면의 특성에 따라서 말입니다. 이것은 다음과 같이 주목할 가치가 있습니다. (It is worth noting) 모든 매체는 충분히(sufficiently) 먼 거리에 걸쳐 빛을 어느 정도 산란시키는 것 말입니다.

세 번째 유형의 빛과 물질의 상호작용은, emission(방사)입니다. 방사 물질은 바꿉니다. 다른 형태의 에너지에서 빛으로 말입니다. 마치 텅스탠 전구 같습니다. 방사물질은 음영 처리와는 관련 없습니다. 광원(light sources)은 종종 수학적으로 모델링 됩니다.

투과도(Transmittance)

빛의 산란(Scattering)

물리학 기반 음영 처리는 대개 빛의 방사와 흡수를 고려하지 않습니다. 하지만 빛의 산란은 고려합니다. 대개의 경우 빛의 산란의 행동은 매우 복잡합니다. 그리고 분석적으로(analytically)풀 수 없습니다.

운좋게도, 음영 목적을 위해 유일한 중요한 경우는(for shading purposes the only important case is) 무한 평면 경계에서의 산란입니다. 왜냐하면 물질의 표면에 미세한 융기(microscopic bumps)가 있어도, 빛의 파장(wavelength)에 대해 무한하고 평면으로 취급할 수 있습니다. 이 경우에, 빛은 모든 방향으로 산란되지 않습니다. 하지만 각 ray(광선)는 정확히 두개로 분리됩니다. reflected(반사)와 refracted(굴절)로 말입니다. 반사의 각은 투사(incidence)각 과 같습니다. 굴절각은 Snell`s law에 의해 정의됩니다.

\[\sin \theta _r=\frac{n_1\sin \theta _i}{n_2}\]

\(n_1\)과 \(n_2\)는 각기(respectively) \(material\ 1\)과 \(material\ 2\)의 굴절 지수 입니다. 이 광선 사이의 에너지는 보존됩니다. 반사와 굴절 광선의 에너지 합은 입사 광선의 에너지와 같습니다.(다를 수도 있음) 굴절과 반사사이의 에너지 비율은 Fresnel equations에 의해 정의됩니다.

프레넬 방정식(Fresnel equations)

프레넬 방정식(Fresnel equations) 또는 프레넬 공식(Fresnel`s formulas)은 반사계수와 투과계수에 관한것으로 한 매질과 광학적 특성 즉, 굴절률이 다른 매질의 계면에서 반사 또는 투과 진폭을 입사진폭으로 나눈 값을 말한다.

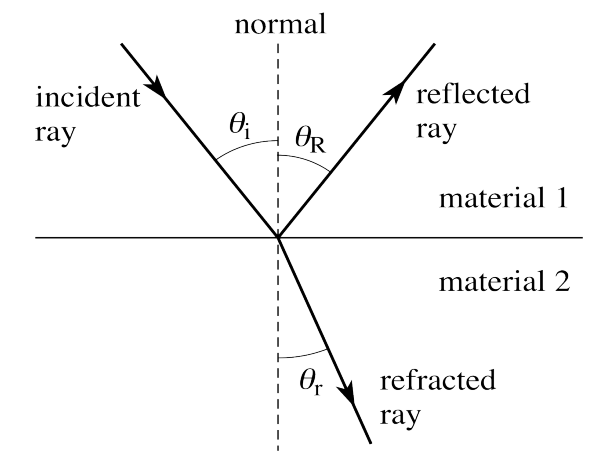
Fresnel equation

광선 \(incident\ ray\) 방향의 입사 평면파는 점 \(O\)에서 굴절률 \(n_1\) 및 \(n_2\)의 두 매질 사이의 인터페이스에 충돌합니다. 파동의 일부는 \(reflected\ ray\)방향으로 반사되고 일부는 \(refracted\ ray\)방향으로 굴절됩니다. 입사광선, 반사광선 및 굴절광선이 결계면의 법선에 대해 이루는 각도는 각각 \(\theta_i\), \(\theta_r\) 및 \(\theta_t\)로 지정됩니다. 이 각도 사이의 관계는 반사 법칙에 의해 제공됩니다.

\[\theta_i=\theta_r\] \[n_1\sin\theta_i = n_2\sin\theta_r\] \[\sin \theta_i = \frac{ n_1 \sin \theta_r }{ n_2 }\]

반사(Reflection)

현실세계에서, 거울과 같이 정확하게 평평한(polished) 표면을 가지고 있지 않습니다. 대부분은 미세한 융기를 가지고 있습니다. 융기는 픽셀보다 작습니다. 하지만 빛의 파장보다는 깁니다. 이러한 종류의 표면은 미세한 광학적(optically)으로 평평한 표면의 대규모 집합으로 모델링됩니다. 각각의 작은 표면의 빛의 반사는 다른 각을 가집니다.

PBR모델에서 이러한 표면특성을 파라메터화 하면 러프니스(Roughness)라 합니다. 표면이 광학적으로 평면일 경우, 러프니스 파라메터값은 0입니다. 반면 값이 1이라면 최대 러프니스 값을 가리킵니다.

양방향 반사도 분포 함수(BRDF, Birdrectional reflectance distribution function)

주요 방상량은 쉐이딩을 위해서 사용됩니다. 방사량을 위해서요. (symbol L). 비록 방사는 스팩트럼 양입니다. 랜더링 목적으로 대부분 RGB 세개로 저장되는 것 말이죠. 방사가 나가는 특정 지점(\(L_0\))는 방사가 들어오는 지점(\(L_i\))의 함수입니다. 이 모델은 대개 사용됩니다. reflectance equation을 묘사하기 위해서요.

\[L_0\left(w_0\right)=\int _{\Omega }^{\ }f\left(w_0,\ w_i\right)\otimes L_i\left(w_i\right)\left(\underline {n\cdot w_i}\right)dw_i\]

나가는 방사는 \(w_0\)로 주어집니다. 지역 조명 세이딩을 위한 \(w_0\)는 view vector v입니다. 이는 쉐이딩 포지션의 카메라에서 가리키는 단위 벡터입니다. 들어가는 방사인 \(w_i\)는 빛의 벡터 입니다. 라이트 소스에서 쉐이딩 포지션으로 가리킵니다. 정수(integral) 오메가는 노말 \(n\)으로 정의되는 반구입니다.

이 공식에서, 반구로 들어오는 모든 방사의 합과 나가는 방사, 즉 들어오는 광선과 표면의 노말의 각으로 가중된 들어오는 모든 방사들은 Bidrectional reflectance distribution function(양방향 반사도 분포 함수, BRDF)로 가중됩니다. 이 함수는 나가는 광선을 가지고, 최종적으로 나가는 방사에 대해서 들어오는 광선이 얼만큼 기여하는지를 구합니다.

BRDF는 scatter에 대한 특정한 분산이나 들어오는 빛의 반사로 표현됩니다. 이는 4개의 각으로 파라메터화 됩니다. 이는 물리적으로 그럴듯 합니다. BRDF는 반드시 reciprocal이여 합니다.

\[f\left(w_0,\ w_i\right)=f\left(w_i,w_0\right)\]

그리고 에너지가 보존되어야 합니다.

\[\forall w_i,\ \int _{\Omega }^{\ }f\left(w_0,w_i\right)\left(\underline {n\cdot w_i}\right)dw_0\le 1\]

가능한 모든 나가는 방향 \(w_0\)에 대해 코사인 계수를 곱한 BRDF의 적분은 가능한 모든 들어오는 방향 \(w_i\)에 대해 1을 초과해서는 안됩니다. 이것은 다음과 같은 간단한 의미입니다. 나가는 모든 빛의 양은 들어오는 모든 빛의 양을 초과해서는 안된다입니다. reflection과 subsurface scattering은 매우 다른 현상입니다. 그리고 가끔 BRDF에서 분리하여 모델링 되기도 합니다.

subsurface scattering을 묘사하는 용어는 specular입니다. 실시간 shading을 위한 두개의 가장 일반적인 BRDF를 설명합니다. 첫번째는 diffuse를 위한 Lambert`s BRDF와 specular를 위한 Cook-Torrance BRDF입니다.

Cook-Torrance specular BRDF

표면 법선 \(n\)이 \(l\)과 \(v\)사이의 절반 벡터 \(h\)와\(\)동일한 미세면만이 반사에 기여할 수 있습니다.

Cook-Torrance specular BRDF는 1981에 만들어 졌습니다. 그리고 필름 렌더링과 off-line 렌더링에 널리 이용되었습니다. 최근에 그래픽 프로세스는 Cook-Torrance model을 실시간으로 실행시킬 수 있을 만큼 발전했습니다. 이로인해 전방위 적으로 PBR을 비디오 게임에서 실시간으로 돌리는 결과를 가져왔습니다.

Cook-Torrance BRDF는 microfacet theory에 바탕을 두고 있습니다. 이 이론에서 표면은 광학적으로 평평한 작은 표면의 집합으로 다룹니다. 각각의 이 microfacets는 normal \(n\)을 가집니다. 뿐만 아니라(futhermore) 표면의 한 점을 쉐이딩 할 때, 들어오는 빛의 벡터는 \(l\)입니다. 그리고 나가는 방향은 \(v\)입니다. 계산해야 하는 것은 \(v\)방향에서 반사되는 \(l\)방향에서 오는 빛의 비율입니다. 표면 법선 \(n\)이 \(l\)과 \(v\)사이의 절반 벡터 \(h\)와\(\)동일한 미세면만이 반사에 기여할 수 있습니다.

Microfacet로 들어오고 microfacet로 나가는 빛은 근처의 기형의 표면에 의해 방해받습니다. 이 현상은 shadowing 그리고 masking으로 각각 불립니다. shadowed 그리고 masked된 microfacets는 반사에 기여하지 않습니다. 모든 반사에 기여하는 microfacets는 active microfacets로 불립니다. Cook-Torrance BRDF는 이러한 가정들로 부터 나옵니다. 그리고 다음의 공식을 따릅니다.

\[f_{Cook-Torrance}\left(v,\ l\right)=\frac{F\left(l,h\right)G\left(l,v,h\right)D\left(h\right)}{4\left(n\cdot l\right)\left(n\cdot v\right)}\]

이 방정식에서, \(F\)는 Fresnel reflectance 항입니다. \(G\)는 shadowing and masking 항입니다. \(D\)는 normal distribution 항입니다. 그리고 분모는 노말라이즈 팩터입니다.

Fresnel reflectance

프랜실 방정식은 빛의 행동을 묘사합니다. 다양한 지수적 반사를 가지며 materials를 통과할 때를요. shading 목적으로, Frsnel항은 반사되는 빛의 양으로 계산됩니다. 빛의 입사각과 재료의 굴절률의 함수로요. 각이 0도일때 각각의 재료의 반사는 특정 양의 빛을 반사합니다. 이것은 기본 반사율 입니다. 45도 각도에서 반사율은 비교적 일정하게 유지됩니다. 그리고 90도에 가까워지면 빠르게 100%에 가까워집니다.

이 현상의 근사값을 사용하는 모델은 Schlick`s function이라고 합니다.

\[F_{Schlick}\left(F_0,\theta \right)=F_0+\left(1-F_0\right)\left(1-\cos \left(\theta \right)^5\right)\]

여기서 specular BRDF 및 microfacets의 경우 입사각은 다음과 같습니다.

\[\cos \left(\theta \right)=l\cdot h\] \[F_{Schlick}\left(F_0,l,h\right)=F_0+\left(1-F_0\right)\left(1-\left(l\cdot h\right)^5\right)\]

어떤 물질의 기본 반사는 들어오는 빛의 파장(wave length)의 함수가 일 수 있습니다(be). 이 현상은 금이나 구리의 색을 부여합니다(gives). PBR에서 \(F\)의 RGB 삼중항(triplet (term))으로 모델링 됩니다.

Normal distribution term

Normal 분포 항, NDF는 스칼라 함수(0개 이상의 파라메터를 받아 단 하나의 값을 반환하는 함수)입니다. h 방향으로 향하는 미세면 법선의 백분율을 제공하는 함수요. (that gives the percentage of microfacet normals oriented towards the direction h) 이 퍼센테이지는 높아지는 경향이 있습니다. h가 macroscopic surface의 노말 n으로 가까워 질 수록이요.

노말 분포의 함수 모델은 표면의 roughness로 파라메터화 됩니다. 보통요. alpha(roughness) 값은 0~1사이의 값입니다. NDF는 에너지를 보존하기위해 노말라이즈 팩터를 가지고 있어야 합니다. 다음의 제약으로 부터 파생된 노말라이즈 팩터요. (NDF가 파생됬다는 건가? 노말라이즈 팩터가 파생되었다는 건가?)

\[\ \int _{\Omega }^{\ }D\left(h\right)\left(\underline {n\cdot h}\right)dw_i=1\]

등방성(isotropic)의 경우 모든 NDF모델의 노말라이즈 팩터는 다음과 같습니다. 가장 자주 이용되는 NDF모델은 Trowbridge-Reitz GGX입니다. (? 어떻게 도출했는지 도저히 모르겠네. 지금은 넘어가야 하나?)

\[isotropic\ case\ NDF`s\ normalization\ factor\ =\ \frac{1}{\alpha ^2\pi }\] \[D_{GGX}\left(h,\alpha \right)=\frac{\alpha }{\pi \left(\left(n\cdot h\right)^2\left(a^2-1\right)+1\right)^2}\]

다른 중요한 모델은 Beckmann` NDF입니다.

\[D_{Beckmann}\left(h,\alpha \right)=\frac{1}{\pi \alpha ^2\left(n\cdot h\right)^4}\exp \left(\frac{\left(n\cdot h\right)^2-1}{\alpha ^2\left(h\cdot h\right)^2}\right)\]

이 효과의 roughness parameter는 그림 3.4와 같이 보일 수 있습니다.

Geometric term

기하학적(? Geoemtric) 또는 shadow masking 항은 다음과 같은 개연성 있는 output의 함수입니다. 주어진 normal h를 가지는 미세면은 들어오는 빛을 나가는 빛의 방향으로 반사할 수 있습니다. 다른말로 probability는 microfacets는 다른 microfacets로 마스크 되거나 쉐도우 되지 않는다 입니다. (오우,,, 이해 못함. 왜요?) NDF에서는 다양한 이론적 모델이 있습니다. 가장 중요한 모델은 Smith`s function입니다. G를 들어오는 빛과 보이는 부분으로 나눈 모델요.

\[G_{Smith}\left(l,v,h\right)=G_1\left(l\right)G_1\left(v\right)\]

G_1은 GGX같은 다른 모델이 될 수 있습니다.

\[G_{GGX}\left(e\right)=\frac{2\left(n\cdot e\right)}{\left(n\cdot e\right)+\sqrt{a^2+\left(1+a^2\right)\left(n\cdot e\right)^2}}\]

또는 Beckmann에서는

\[c=\frac{n\cdot e}{\alpha \sqrt{1-\left(n\cdot e\right)^2}}\] \[G_{Beckmann}\left(e\right)=\begin{cases}3.535c\ +2.181c^2&if\ c<1.6\ \\1&if\ c\ \ge 1.6\end{cases}\]

이것으로 cook-torrance specular BRDF의 분석이 완료되었습니다. 벡만과 GGX항과 다른점은 다음 그림 3.5, 3.6 그리고 3.7에서 볼 수 있습니다.

Lambert`s diffuse BRDF

실시간 렌더링에서, 가장 자주 사용되는 diffuse BRDF는 Lambert`s BRDF입니다.

\[f_{Lambert}\left(v,l\right)=\frac{c_{diff}}{\pi }\]

이 BRDF는 사실 상수입니다. 무슨 뜻이냐면, 균일한(uniform) 확산(diffusion)을 모델링합니다. 들어오는 빛은 가능한 모든 방향으로 똑같이 산란 가능합니다. 이 파라메터는 종종 albedo 또는 diffuse color로 불립니다. 그리고 일반적으로 재료의 색상으로 생각되는 것과 밀접하게 일치합니다. (재료의 색상이 어떻게 diffuse BRDF가 되는지 모르겠는데?)

반사율 방정식에 사용되는 BRDF는 Specular와 Diffuse BRDF로 구성(consists)됩니다. 하지만 어떻게 조합되든간에 에너지 보존법칙은 지켜집니다. 이것은 다양한 방법으로 달성될 수 있습니다. 가장 평범한 방법으로는 BRDF요소 간의 선형 보간을 통해서 할 수 있습니다. 어떤 계수(factor)냐면 주어진 음영 지점에서 물체의 반사율에 비례(proportional)하는 계수요. 이 성질을 만족시키는 인자는 diffuse Fresnel 항입니다.

\[\cos \left(\theta \right)=v\cdot n\] \[F_{diff}\left(F_0,v,n\right)=F_0+\left(1-F_0\right)\left(1-\left(v\cdot n\right)^5\right)\]

마지막으로, 전체 BRDF는

\[f\left(v,l\right)=f_{Lambert}\left(v\cdot l\right)\left(1-F_{diff}\right)+f_{Cook-Torrance}\left(v,l\right)F_{diff}\]

그림 3.8에서 F_0의 값은 왼쪽 0에서 오른쪽 1로 변합니다. diffuse와 roughness는 유지된 채로요. 구체의 모양이 유전체에서 금속으로 어떻게 변하는지 볼 수 있습니다.(It can be seen how the sphere`s appearance changes from dieletric to metallic)

거칠기(Roughness)

러프니스는 머티리얼 표면이 거칠거나 부드러운 정도를 제어합니다. 머티리얼에서 러프니스 입력은 머티리얼에 나타나는 리플렉션이 얼마나 희미하거나 선명한지를 결정합니다. 이는 표면이 사람의 눈이나 촉감에서 감각과 같게 보인다는 점에서 주목할 만합니다.

거친 재질에 반사된 빛은 부드러운 재질보다 여러 방향으로 퍼져 분산되며, 가끔 미세한 반사가 나타나기도 합니다. 매끄러운 표면에서는 빛이 더 균등하게 반사되므로 선명하고 집중된 리플렉션 또는 스페큘러 하이라이트가 나타납니다.

비금속 러프니스에 따른 변화

굴절(Refraction)

물질의 흡수력과 구성이 빛의 굴절이 일어나는 일을 결정합니다. 금속은 매우 높은 흡수력을 가지고 있어서 물질에서 나오는 굴절이 없습니다. 반대로 유리는 매우 낮은 흡수율을 가지고 있습니다. 따라서 굴절된 빛은 볼륨을 흡수 없이 온전히 통과할 수 있습니다.

두개의 극단적인 유전체물질에서, 유전체는 일정량의 빛을 흡수합니다. 하지만 유리와 같이 구성물들은 빛이 물질을 방해받고 통과하는 것을 허용하지 않습니다. 대신에 빛은 입자에 대하여 오브젝트의 표면 아래에서 산란합니다. 그리고 일부의 빛은 같은 표면으로 다시 나가게 됩니다. 이러한 현상을 Subsurface scattering 또는 Diffusion이라고 합니다.

유전체(dielectric material)는 전기장 안에서 극성을 지니게 되는 절연체입니다.

Subserface scattering

Subsurface scattering

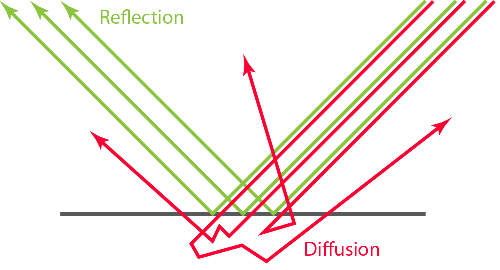
Diffusion

Diffusion

쉐이딩에서 디퓨전을 모델링하는 것은 표면 아래에서 산란하는 크기에 의해 결정됩니다. 만일 모든 거리가 (모든 광선이 표면에서 들어오는 진입과 나가는 부분까지의 거리) 픽셀보다 작다면, 지역적으로 Diffusion을 계산할 수 있습니다. 아니라면, 예를 들어 사람의 피부와같은, 왁스 또는 충분히 얇은 유전체 물질등은 특별한 non-local subsurface scattering 랜더링 기술이 필요합니다.

메탈릭(Metallic)

메탈릭(Metallic) 입력은 0과 1사이의 값을 받으며, 머티리얼이 금속인지, 비금속인지를 정의합니다.

언리얼 엔진에서는 메탈릭을 바이너리 프로퍼티로 취급하는 경우가 대부분입니다. 순수한 금속, 돌, 플라스틱 등 순수한 표면의 경우, 메탈릭을 0과 1사이의 값이 아닌 0또는 1로 설정해야 합니다. 부식되었거나, 먼지가 쌓였거나, 녹이슨 금속과 같은 혼합 표면을 만들 때는 0과 1사이의 값이 필요할 수 있습니다.

비금속의 메탈릭 값은 0입니다. 0이 기본값입니다.
금속의 메탈릭 값은 1입니다.

Metallic

Specular

언리얼에서 스페큘러(Specular) 입력은 0과 1 사이의 값을 받으며, 표면에 스페큘러 라이트가 반사되는 정도를 제어합니다.

스페큘러 값이 0이면 반사가 없습니다.
스페큘러 값이 1이면 완전히 반사됩니다.

언리얼 엔진이 사용하는 기본 스페큘러 값 0.5는 약 4%의 스페큘러 리플렉션을 나타냅니다. 이 값은 대부분 머티리얼에서 정확하게 작용합니다.

디퓨즈가 매우 심한 머티리얼은 스페큘러 값을 0으로 설정하고 싶을 수 있지만, 참아야 합니다! 모든 머티리얼에는 스페큘러가 있습니다. 디퓨즈가 심한 머티리얼을 만드는 올바른 방법은 러프니스 값을 올리는 것입니다.

지식의 확장

Gamma and high dynamic range

자세한 구현을 하기 전에, gamma correction과 high dynamic range가 강조되어야 합니다.

Gamma correction

텍스쳐는 비선형화된 sRGB 공간에 인코딩한 color data를 가집니다. 이 것은 인간이 보기에 더 적합합니다. 이러한 텍스쳐는 쉐이딩 방정식에 입력되기 전에 선형화 되어야 합니다. 그렇지 않으면 결과는 정확하지 않습니다. 유사하게, 최종 칼라 데이터는 반드시 모니터를 통해서 사용자가 보기위해 출력되기 전에 gamma corrected되어야 합니다. 이 gamma correction 효과는 그림 4.1에서 볼 수 있습니다. 왼쪽 그림에서 lit과 unlit의 영역의 바운더리가 너무 부드럽습니다.

선형화는 색상 값을 감마의 거듭제곱으로 올려서 수행됩니다. 또는 감마 보정의 경우 감마의 역수로 값을 올립니다.

High dynamic range

화창한 날, 태양에서 오는 빛의 밝기는 수천배더 강합니다. 다른 광원의 강도보다요. 이러한 폭넓은 밝기는 8bit 빛 축적 버퍼에서 모델링 하는 것이 불가능합니다. 이러한 문제는 high dynamic range를 이용하여 풀 수 있습니다. 8bit per channel 대신 16bit 또는 더 거대한 부동 소수점 버퍼를 이용해서요. 8비트 버퍼와 다르게 부동소수점 버퍼는 값을 1보다 더 크게 할 수 있습니다. 빛의 축적 단계 후, 언바운드된 버퍼값은 반드시 [0,1]범위에 리맵되어야 합니다. 모니터에 출력되기 위해서요. 함수는 이러한 달성을 톤 맵핑이라 부릅니다. 예를 들면 다음과 같습니다.

\[T\left(c_{hdr}\right)=1-\exp \left(-c_{hdr}\cdot \exp osure\right)\]

이러한 exposure파라메터는 phtography i.e의 exposure와 유사(analogous)합니다. 단위 면적당 빛의 총량 같은거요. 이러한 파라메터는 스크린 화면의 밝기 총량의 평균으로부터 도출할 수 있습니다. 또는 조정(tweaking, 이미지랑 일치 하지 않는데, 부정적인 느낌의 조정인가?)을 위해 아티스트에게 맡길 수 있습니다. HDR의 효과와 톤 맵핑은 그림 4.2와 같이 묘사될 수 있습니다.

블림 퐁 모델과의 비교

PBR쉐이딩 모델의 경계선은 albedo로 파라메터화 될 수 있습니다. specular, surface, rougness로요. 비록 블림 퐁 모델은 유사하게 diffuse, specular 그리고 glossiness로 파라메터화 하지만, 이 파라메터그룹은 매우 다른 의미를 가지고 있습니다. 다음과 같은 이유로요. 같은 파라메터를 각각의 모델이 입력하고 결과를 비교했을 때 유효하지 않습니다. 각 모델이 생성할 수 있는 그래픽 충실도를 완전히 활용하려면 각 모델에 대해 별도의 매개변수 세트를 만들어야 합니다.(??? A separate set of parameters should be made for each model in order to fully utilize(활용하다, 이용하다) the graphical fidelity(충실도? 충실) each model can produce)

더 나아가, 두 모델을 비교하는 절대적인 방법은 없습니다. 비교는 일반적으로 렌더링된 이미지의 인지된 시각적 정확성을 비교하여 이루어집니다. 내 메모와 함께 그림 4.6에서 4.8은 각 모델로 렌더링된 동일한 장면을 나타냅니다.

Implementing PBR

Solving the reflectance equation

이 섹션은 가능한 해결법과 랜더링 방정식의 근사치를 제공합니다.

Punctual light sources

반사 방적신을 완전히 풀기 위해서는, normal-defined hemisphere 주변의 빛이 들어올 수 있는 모든 방향의 들어오는 빛은 적분되어야 합니다. 이거는 명백하게 실시간으로 불가능합니다. 이 방정식은 punctual light sources로 풀수 있습니다. 포인트 라이트, spot 라이트 방향 라이트 같은 것들로요. punctual light로 lit되는 것은 쉐이딩 포인트는 단 하나의 방향 l_c로 부터 빛을 받습니다.

\[\left(4.1\right)\ \ \ \ L_i\left(l\right)=0,\ \forall l\ne l_c\]

(3.1)에 (4.1)을 적용함으로써 적분을 제거할 수 있습니다.

\[L_0\left(w_0\right)=\int _{\Omega }^{\ }f\left(w_0,w_i\right)\otimes L_i\left(w_i\right)\left(\underline {n\cdot w_i}\right)dw_i\ \leftarrow \ L_i\left(l\right)=0,\ \forall l\ne l_c\] \[\left(4.2\right)\ \ \ \ L_0\left(v\right)=f\left(v,l_c\right)\otimes L_i\left(l_c\right)\left(\underline {n\cdot l_c}\right)\]

Punctual lights는 c_light로 파라메터화 됩니다. 표면 법선에 수직인 방향의 빛이 비추었을 때 흰색 램버시안 표면의 색상입니다. (뭔소린지??, the color a white lambertian surface would have when lit by the light from the direction perpendicular to the surface normal.)

\[\left(4.3\right)\ \ \ \ l_c=n\] \[\left(4.4\right)\ \ \ \ c_{light}=\int _{\Omega }^{\ }f_{Lambert}\left(v,w_i\right)\otimes L_i\left(w_i\right)\left(\underline {n\cdot w_i}\right)dw_i\]

(3.2)를 (4.4)에 c_diff=1과 함께 대입하면, ((3.2)가 뭐드라???)

\[\left(4.5\right)\ \ \ \ c_{light}=\frac{1}{\pi }\int _{\Omega }^{\ }L_i\left(w_i\right)\left(\underline {n\cdot w_i}\right)dw_i\]

(4.1)과 (4.3)을 (4.5)에 적용하면.

\[c_{light}=\ \frac{1}{\pi }L_i\left(l_c\right)\] \[L_i\left(l_c\right)=\pi c_{light}\]

(4.7)을 (4.2)에 집어넣으면 punctual light shading equation의 최종 결과를 얻습니다.

\[L_o\left(v\right)=\pi f\left(v,l_c\right)\otimes c_{light}\left(\underline {n\cdot l_c}\right)\]

이 방정식은 모든 scene위에 있는 punctual light에 대해 각각 계산되어야 합니다. 그리고 결과는 더해져야 합니다. 빛 감쇠(attenuation)을 모델링하기 위해서는, c_light를 광원까지의 거리 함수로 만들 수 있습니다.

\[c_{light}\left(d\right)=\frac{c_{light_0}}{a_0d^2+a_1d+a_2}\]

Indirect lighting

신에 punctual light만으로 빛을 비추면 문제가 있을 수 있습니다. 빛이 비춰지지 않는 영역은 완벽하게 어둡습니다. 비슷하게, 높은 specular 오브젝트는 거의 빛을 산란합니다. 표면 노말이 라이트벡터에 대해 높은 각을 가지고 있을 때요. 이러한 문제는 그림 4.3에서 볼 수 있습니다.

이러한 문제의 가능한 해결책은 ambient 그리고 환경에 기반이 되는 빛을 가지는 것입니다. ambient lighting은 쉽게 추가될 수 있습니다. 쉐이딩 결과의 상수 값으로요. 신의 밝기를 위해서요. 하지만 이러한 접근은 매력적인 결과를 출력하지 못합니다.

다른 방법으로는, environment lighing techniques는 좋은 결과를 만들 수 있습니다. environment cube map(sky box)는 radiance map으로 다뤄질 수 있습니다. 각각의 radiance map의 픽셀은 무한히 멀리있는 빛으로 표현될 수 있습니다. 그리고 c_light는 픽셀의 칼라가 될 수 있습니다. 이 arguments와 lambert`s BRDF를 적용할 때, 반사 공식은 sourface normal에 대한 함수가 됩니다.(By applying these arguments and Lambert`s BRDF, the reflectance equation becomes a function of only the surface normal, 얼 추 비슷하게 번역했나????)

I는 조사(irradiance)입니다. n의로 정의된 반구와 만나는 모든 들어오는 빛의 합입니다. 이 값은 다양한 값 n에 의해 미리 계산될 수 있습니다. 이 미리 계산된 결과는 irradiance map에 저장될 수 있습니다. 텍스처 좌표t에서 I(t)값을 갖는 큐브맵으로요. (a cube map that has the value of I(t)at texture coordinates t)

I를 계산하기 위해서, 방정식 (4.10)은 polar coordinates로 표현됩니다.

\[\left(4.11\right)\ \ \ \ I\left(n\right)=\frac{1}{\pi }\int _{\varphi }^{\ }\int _{\theta }^{\ }L_i\left(\varphi _i,\theta _{i\ }\right)\cos \left(\theta _i\right)\sin \left(\theta _i\right)d\theta _id\varphi _i\]

적분은 Monte Carlo 적분을 각각적용하여 풀 수 있습니다.

\[\left(4.12\right)\ \ \ \ I\left(n\right)=\frac{1}{\pi }\ \frac{2\pi }{N_1}\ \frac{\pi }{2N_2}\sum _{\ }^{N_1}\sum _{\ }^{N_2}L_i\left(\varphi _i,\theta _i\right)\cos \left(\theta _i\right)\sin \left(\theta _i\right)\] \[\left(4.13\right)\ \ \ \ I\left(n\right)=\frac{\pi }{N_1N_2}\sum _{\ }^{N_1}\sum _{\ }^{N_2}L_{i\ }\left(\varphi _i,\theta _i\right)\cos \left(\theta _i\right)\sin \left(\theta _i\right)\]

N_1과 N_2는 각 각의 샘플 넘버입니다. 들어오는 radiance L_i는 t에 대한 방사맵 테긋쳐 좌표의 샘플 입니다.

\(t=\left(\sin \left(\theta \right)\cos \left(\varphi \right),\sin \left(\theta \right)\cos \left(\varphi \right),\cos \left(\theta \right)\right)\) 조사(irradiance)맵핑의 효과는 그림 4.4에서 볼 수 있습니다. 빛이 비춰지지 않는 영역은 환경 맵에서 조명을 받는 것을 볼 수 있습니다.

specular image를 미리 계산하는 것은 불가능하지 않습니다. 뷰 다이렉션에 대해 의족적인 빛을 바탕으로둔 스펙큘라 이미지를요. 이 경우에, 방사맵은 런타임에 샘플됩니다. 그리고 specular BRDF는 각각의 샘플을 계산해야 합니다. 그러나 이것은 실시간 어플리케이션에서 불가능합니다. 종종 대안으로 스펙큘라 오브젝트에 대한 환경맵핑이 계산이 이용됩니다. 그리고 머티리얼의 러프니스값에 의존하여 반사를 블러하는 것도 이용됩니다. 블러링은 밉맵을 계산하는 것을 통해서 달성할 수 있습니다. environment map에 대해서요. 그리고 간단히 선택됩니다. 환경 맵을 샘플링하는 동안 픽셀의 러프니스 값을 바탕으로 밉맵 레벨을 선택하는 것을요. 이 방법의 결과는 그림 4.5에서 볼 수 있습니다. (솔직히 그림보고 무슨 차이인지 모르겠다. ㅎㅎ.)