방향 (Orientation)의 표현
모델의 방향을 나타내기 위해서는 모델만의 좌표축을 사용합니다. 이때 보통 x, y, z라는 이름 대신에 요(yaw), 피치(pitch), 롤(roll)이라는 이름을 사용합니다.
회전과방향을 정확히 구분하면,회전은 행위를 말하고방향은 상태를 의합니다. 더 정확하게 표현하자면 회전은 변환이라는 행위를 나타내고 그 행위를 나타내기 위해 앞에서 아핀 변환 행렬을 사용하는 법을 배웠습니다. 방향은 회전 이전 혹은 이후에 모델이 어떻게 놓여 있는지에 대한 상태를 나타냅니다.
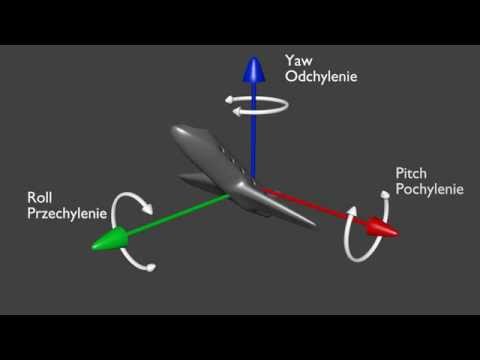
요, 피치, 롤
요, 피치, 롤은 서로에게 수직인 세 개의 단위 벡터라고 할 수 있습니다. 모델의 중심 점과 이 세개의 단위 벡터를 통해서 모델만의 좌표계를 만들 수 있습니다. 이것을 흔히 로컬 좌표계(local coordinate)라고 합니다.
모델의 로컬 좌표계의 세 축, 요\((Y_x, Y_y, Y_z)\), 피치\((P_x, P_y, P_z)\), 롤\((R_x, R_y, R_z)\)이 바로 모델의 방향을 나타낸다고 할 수 있습니다. 이 세단위 벡터들은 열벡터로 써서 다음과 같이 행렬로 나타낼 수 있습니다.
\[\begin{bmatrix} Y_x & P_x & R_x \\ Y_y & P_y & R_y \\ Y_z & P_z & R_z \end{bmatrix}\]- 이 세 열벡터들이 단위 벡터이며, 서로에게 수직입니다. 따라서 위 행렬은 자련스럽게 회전 변환을 나타내는 행렬이 됩니다.
- 이 말은 회전과 방향은 엄연히 다른 의미이지만 그들을 표현하는 방식이 서로 같을 수 있다는 것입니다.
표현법에 따른 수식만을 가지고는 이것이 어떤 모델을 회전을 하려고 하는 것인지 아니면, 모델의 방향을 나타낸 것인지 알 수 없으므로, 때에 따라 분명히 해줘야 할 것입니다.
오일러 각(Euler Angles)
임의의 한 회전 혹은 여러 회전의 조합은 결국 하나의 축과 그 축을 중심으로 얼마나 회전할지를 나타내는 각으로 표현할 수 있습니다. 이때 기준이 되는 축을 오일러 축(Euler axis)이라고 부르며 보통은 단위 벡터로 나타냅니다.
- 이 방식을 흔히 축-각(axis-angle)방식이라고 부릅니다.

Axis-Angle
오일러의 회전 정리(Eulers rotation theorem)에 따르면, 임의의 한 회전 혹은 여러 회전의 조합은 결국 하나의 축과 그 축을 중심으로 얼마나 회전할지를 나타내는 각으로 표현할 수 있습니다. 이때 기준이 되는 축을 오일러 축(Euler axis)이라고 부르며 보통은 단위 벡터로 나타냅니다.
만약 벡터 \(v\)가 하나의 회전 혹은 여러 번의 회전을 거쳐 최종적으로 벡터\(v`\)가 되었다고 해보면, 이때 우리는 항상 \(v\)와 \(v`\)에 수직인 단위 벡터 \(\hat{k}\)를 두 벡터를 외적하고 그 결과를 정규화해서 구할 수 있습니다. 또한 \(v\)와 \(v`\)사이각 \(\theta\)는 두 벡터를 정규화해서 내적을 하고, 그 결과에 \(cos\)의 역함수, \(arccos\)함수를 적용하면 구할 수 있습니다.
\[\hat{k} = \frac{v \times v`}{\| v \times v \|}\] \[\theta = arccos(\frac{v}{\|v\|} \cdot \frac{v`}{\| v`\|})\]축-각 방식으로 방향을 표현하면 오일러 각과 비슷하게 하나의 단위 벡터 \(\hat{k} = (k_x, k_y, k_z)\)와 회전각 \(\theta\), 총 4개의 성분만이 필요하므로 행렬에 비해 메모리를 적게 쓰는 장점이 있습니다.
\[R_{axis-angle} = (k_x, k_y, k_z, \theta)\]이 방식의 기본적인 아이디어는 회전하려는 벡터를 회전축에 평행한 성분과 수직인 성분으로 쪼개고, 수직인 성분을 회전시킨 후 이를 다시 평행인 성분과 결합하는 것입니다. 이렇게 벡터 \(v`\)는 다음과 같이 구할 수 있습니다.
\[v` = cos \theta \cdot v + (1 - cos \theta) \cdot (v \cdot \hat{k}) \cdot \hat{k} + sin \theta \cdot (\hat{k} \times v)\]- d이 식을 처음 소개한 사람은 프랑스 수학자인 로드리게스(Benjamin Olinde Rodrigues)입니다. 그의 이름을 따서
로드리게스 회전 공식(Rodrigues rotation formula)라고 불립니다.
사원수 (Quaternion, 쿼터니언)
3차원 그래픽에서 회전을 표현할 때, 행렬 대신 사용하는 수학적 개념으로 4개의 값으로 이루어진 복소수(Complex Number)체계입니다.
\[q = <w, x, y, z> = w + xi + yj + zk\]- 실수부와 허수부의 합으로 구성된 수입니다.
- 사원수는 행렬에 비해 연산 속도가 빠르고, 차지하는 메모리의 양도 적으며, 결과의 질에 있어 오류가 날 확률이 적습니다.
- 3개의 축에 대한 회전 연산을 동시에 적용하는 경우에 행렬을 사용하면 한 축이 소실되는 짐벌락 현상이 발생할 수 있습니다. 사원수를 사용하면 이 현상을 막을 수 있습니다. (완벽하게 막지는 못합니다.)
10 mins GameDev tips - Quaternions
쿼터니언의 각 값이 나타내는 현상입니다.

사원수의 정의
사원수는 4차원 복소수 공간(Complex Space)의 벡터로서 다음과 같이 나타냅니다.
\[q = <w, x, y, z> = w + xi + yj + zk\]사원수를 \(q = s + v\)형태로 쓰기도 하는데, 여기서 s는 q의 w성분에 해당하는 스칼라(Scalar)값이고, v는 q의 x, y, z 성분에 해당하는 벡터(Vector) 부분입니다.
사원수의 특징
사원수의 곱은 일반적인 분배법칙을 따르며 허수 성분인 i, j, k는 다음과 같은 특징을 갖습니다.
\(i^2 = j^2 = k^2 = -1\)
\(ij = -ij = k\)
\(jk = -kj = i\)
\(ki = -ik = j\)
추가적으로 각 원소가 어떤 의미를 가지는지 볼 수 있습니다.
언리얼 블루프린트에서 쿼터니언 구하기
에서, 쿼터니언을 기본적으로 제공해 주지 않는 이유를 설명합니다… 중요한건 블루프린트에서 쿼터니언을 사용하고자 한다면, Rotation을 Vector로 변환 후 EulerVector로 부터 Quaterion을 만들 수 있다는 점 입니다.
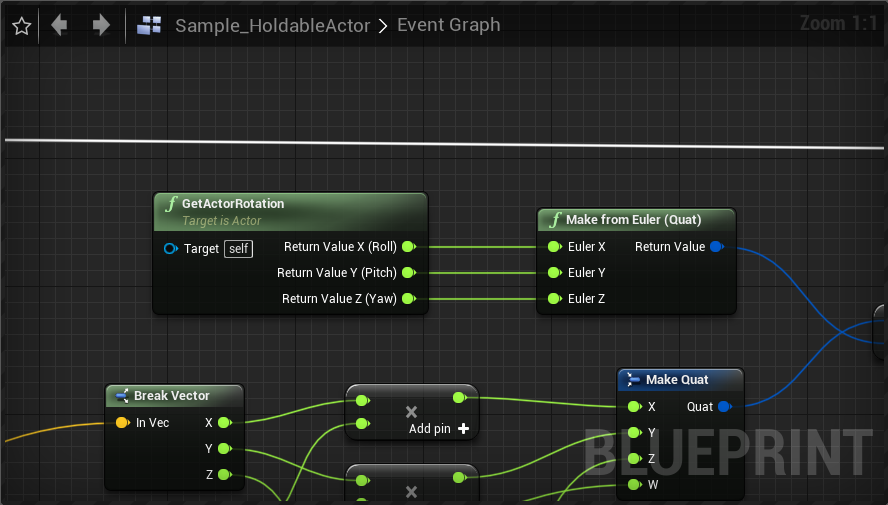
축과 각도로 부터 쿼터니언 구하기
축 A에 대한 각도 Θ 만큼의 회전을 사원수로 나타내면 다음과 같습니다.
q = cos(Θ/2) + A sin(Θ/2)
사원수를 회전행렬로 변환하면, 아래와 같습니다.
| 1-2y^2-2z^2 2xy-2wz 2xz+2wy 0 |
R_q = | 2xy+2wz 1-2x^2-2z^2 2yz-2wx 0 |
| 2xz-2wy 2yz+2wx 1-2x^2y^2 0 |
| 0 0 0 1 |
Maths - AxisAngle to Quaternion
축과 각도로 부터 쿼터니언은 다음과 같이 구할 수 있습니다.
\(qx = ax * sin(angle/2)\)
\(qy = ay * sin(angle/2)\)
\(qz = az * sin(angle/2)\)
\(qw = cos(angle/2)\)
- 축은 길이가 1입니다. 따라서 길이를 구할 때, qx, qy, qz 성분이 \(sin(angle/2)^2 + cos(angle/2)^2 = 1\)가 되어 정규화된 쿼터니언이 나오게 됩니다.
- Angle이라고 표시되었지만, 실제 계산에서는 대부분 Radian을 사용합니다. Radian/2로 대신할 수 있습니다.
사원수의 곱셉
기존에 있는 회전에 새로운 회전을 더하고 싶다면 다음의 순서를 따라야 합니다. (새로운 회전)*(기존에 있는 회전)로 적용이 됩니다.
두 사원수가 다음과 같으면
\(q1 = w1 + x1i + y1j + z1k = s1 + v1\)
\(q2 = w2 + x2i + y2j + z2k = s2 + v2\)
사원수의 곱셉은 다음과 같습니다.
\(q1q2 = (w1w2 - x1x2 - y1y2 - z1z2)\)
\(+ (w1x2 + x1w2 + y1z2 - z1yy)i\)
\(+ (w1y2 - x1z2 + y1w2 + z1x2)j\)
\(+ (w1z2 + x1y2 - y1x2 + z1w2)k\)
\(= s1s2 - v1·v2 + s1v2 + s2V1 + v1×v2\)
- 사원수는 곱셉의 교환법칙이 성립하지 않습니다.
- 회전 행렬에서 새로운 회전이 앞에가야 하는 이유를 설명합니다.
사원수의 켤레(Conjugate)
사원수 q = s + v의 켤레사원수는 q\hat 라고 표기합니다. q\hat = s - v입니다. 사원수 q와 그의 켤레 q\hat의 곱은 q자신의 내적과 동일합니다. q 자신의 내적 q·q는 q의 크기의 제곱입니다. 즉,
q q\hat = q \hat q = q·q = ||q||^2 = q^2
사원수의 역수
0이 아닌 사원수 q의 역수 q-1는 다음과 같이 주어집니다.
q-1 = q \hat / q^2
그리고 다음과 같은 특징을 같습니다.
q q\hat = q \hat q = 1
사원수의 크기
||q|| = Norm(q) = sqrt(w^2 + x^2 + y^2 + z^2)
사원수의 단위
w^2 + x^2 + y^2 + z^2 = 1
사원수의 정규화 (단위 쿼터니언)
q = q / ||q|| = q / sqrt(w^2 + x^2 + y^2 + z^2)
사원수의 보간(interpolation)
물체의 애니메이션을 수행할 때, 보간을 통해 계산된 키프레임 사이의 중간 방향을 생성합니다.
가장 간단한 보간은 선형보간(linear interpolation)으로 두 개의 값을 점으로 생각하고 두 개의 점을 이어주는 직선의 방정식으로부터 값을 얻어내는 방법입니다.
두 사원수 q1, q2에 대해, 선형 보간된 사원수 q(t)는 다음과 같습니다. 보간 후에는 정규화를 해줘야 합니다.
q`(t) = (1-t)q_1 + tq^2
q(t) = q`(t) / ||q`(t)||
- q1 -> q2를 잇는 선을 따라 보간합니다.
이러한 선형 보간은 간단하고, 효과적이나 호를 일정한 비율로 추적하지 않는다는 문제가 있습니다. 이에 따라 구면 선형보간(sphericcal linear interpolation : slerp)가 나타났습니다.
q(t) = sinΘ (1-t) / sinΘ * q1 + sinΘ t / sinΘs * q^2
- 보간이란 처음과 끝의 값을 가지고 중간에 잇는 값을 계산해 내는 것입니다.
언리얼 쿼터니언
지면에 물건 배치하기
- 두고자 하는 위치의 충돌정보를 구합니다.
- 충돌하는 위치의 노말과 업 벡터가 일치하도록 만드는 회전을 만듭니다.
- 회전을 적용하고, 물건을 배치합니다.
- 물건 즉 액터의 업벡터가 액터의 위쪽 방향을 가르키는 상황을 전제로 합니다.
- 외적은 둔각을 반영하지 못하니, 내적과 외적 둘다 해야합니다.
주요 참고자료 : 쿼터니언 이해하기
