- 벡터와 행렬에서 관계 추가하기
- 행렬에 대한 이해가 부족.
- 선형 변환 조합의 행렬 곱셉
Linear Transformation(선형 변환)
선형 변환은 일반적으로 하나의 벡터 공간을 다른 벡터 공간으로 변환하는 함수라고 할 수 있습니다. 이것이 가능한 이유는 선형 변환을 정의하는 두 특성이 변환 후에도 벡터 공간의 조건을 그대로 만족하기 때문입니다.
- 어떤 벡터를 회전한다고 이야기할 때는 반드시 두 얼만큼 회전할 것인가, 무엇을 기준으로 회전할 것인가를 이야기해야 합니다.
선형 변환과 행렬
선형 변환 \(T\)가 벡터 공간 \(V\)를 다른 벡터 공간 W로 변환한다고 하면, 이때 \(V\)는 \(n\)차원, \(W\)는 \(m\)차원 벡터 공간이라고 하면 다음과 같이 쓸 수 있습니다.
\[T:R^n \rightarrow R^m\]\(V\)의 기저 벡터들에 선형 변환 \(T\)를 적용하는 것을 다음과 같이 표현합니다.
\[\begin{align} T(v) & = T(c_1 \cdot v_1 + c_2 \cdot v_2 + ... + c_n \cdot v_n)\\ & = c_1 \cdot T(v_1) + c_2 \cdot T(v_2) + ... + c_n \cdot T(V_n) \end{align}\]기저 벡터 &&v&&를 변환된 벡터(\(W\))의 기저 벡터 \(w\)로 표현한 후, 이를 기저 벡터 \(w\)로 변환하면 다음과 같습니다.
\[\begin{align} c_1 (a_{1, 1}w_1 + a_{2, 1}w_2 + ... + a_{m, 1}w_m) + \\ c_2 (a_{1, 2}w_1 + a_{2, 2}w_2 + ... + a_{m, 2}w_m) + \\ ... \\ c_2 (a_{1, 2}w_1 + a_{2, 2}w_2 + ... + a_{m, 2}w_m) \end{align}\]이를 다시 기저 벡터 \(w_i\) 중심으로 다시 전개할 수 있습니다.
\[\begin{align} (c_1a_{1, 1}+c_2a_{1, 2}+...+c_na_{1, n})w_1 + \\ (c_1a_{2, 1}+c_2a_{2, 2}+...+c_na_{2, n})w_2 + \\ ... \\ (c_1a_{m, 1}+c_2a_{m, 2}+...+c_na_{m, n})w_m + \\ \end{align}\]기저 벡터 \(b_k\)에 곱해지는 값을 \(b_k\)로 정의한다면
\[b_k=c_1a_{k, 1} + c_2a_{k, 2} + ... + c_na_{k, n}\]\(T(v)\)를 벡터 공간 \(W\)에 있는 벡터 \(w\)를 만들 수 있습니다.
\[T(v)=b_1w_1 + b_2w_2 + ... b_mw_m = (b_1,b_2,...,b_m) = w\]열벡터를 행렬로 바꾸면 다음과 같이 표현될 수 있습니다.
\[\begin{bmatrix} b_1 \\ b_2 \\ ... \\ b_m \end{bmatrix} = \begin{bmatrix} c_1a_{1, 1}+c_2a_{1, 2}+...+c_na_{1, n} \\ c_1a_{2, 1}+c_2a_{2, 2}+...+c_na_{2, n} \\ ... \\ c_1a_{m, 1}+c_2a_{m, 2}+...+c_na_{m, n} \end{bmatrix} = \begin{bmatrix} a_{1, 1} & a_{1, 2} & ... & a_{1, n} \\ a_{2, 1} & a_{2, 2} & ... & a_{2, n} \\ ... \\ a_{m, 1} & a_{m, 2} & ... & a_{m, n} \end{bmatrix} \times \begin{bmatrix} c_1 \\ c_2 \\ ... \\ c_n \end{bmatrix}\]다시 이를 \(W\)의 기저 벡터에 대하여 \(m, n\) 행렬 \(M\)으로 표현할 수 있습니다.
\[w = M \times v\]3차원 공간의 유클리드 벡터에 대한 선형 변환을 다루므로 다음과 같이 표시할 수 있습니다.
\[T:R^3 \rightarrow R^3\] \[\begin{bmatrix} b_1 \\ b_2 \\ b3 \end{bmatrix} = \begin{bmatrix} a_{1, 1} & a_{1, 2} & ... & a_{1, 3} \\ a_{2, 1} & a_{2, 2} & ... & a_{2, 3} \\ a_{3, 1} & a_{3, 2} & ... & a_{3, 3} \end{bmatrix} \times \begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix}\]행벡터를 기준으로 한다면, 다음과 같이 적용됩니다.
\[w^T = v^T \times A^T\]크기 변환(Scaling)
크기 변환은 벡터에 대해서 크기만을 바꾸는 선형 변환이므로 다음과 같이 정의할 수 있습니다.
\[T(v) = (a \cdot v_x,b \cdot v_y,c \cdot v_z)\]3차원 공간의 기저벡터를 다음과 같다고 합니다.
\[i = (1, 0, 0)\] \[j = (0, 1, 0)\] \[k = (0, 0, 1)\]기저벡터에 앞의 크기만을 바꾸는 변환행렬을 적용합니다.
\[T(i) = (a \cdot 1, b \cdot 0, c \cdot 0) = (a, 0, 0)\] \[T(j) = (a \cdot 0, b \cdot 1, c \cdot 0) = (0, b, 0)\] \[T(k) = (a \cdot 0, b \cdot 0, c \cdot 1) = (0, 0, c)\]따라서 크기 변환은 다음 행렬의 모양을 가집니다.
\[M = \begin{bmatrix} T(i) & T(j) & T(k) \end{bmatrix} = \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end{bmatrix}\]이를 이제 행렬 곱셈으로 표현 할 수 있습니다.
- 크기 변환에서 역행렬을 구하는 것은 주 대각 성분을 역수로 만들면 역행렬이 됩니다.
2차원에서 원점을 기준으로 회전
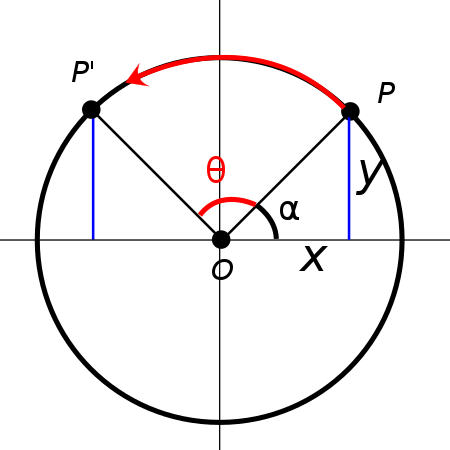
두 점을 변환시키는 회전 행렬을 구할 때, 선형 변환을 구한다면,
먼저 \(x, y\)가 다음과 같을 때
\[x = l \cdot cos(\alpha)\] \[y = l \cdot sin(\alpha)\]x 값에 대해서
\[x = l \cdot cos(\alpha)\] \[x` = l \cdot cos(\alpha + \theta)\] \[x` = l \cdot ( cos(\alpha)cos(\theta) + sin(\alpha)sin(\theta) )\] \[x` = x \cdot cos(\theta) + y \cdot sin(\theta)\]y값에 대해서
\[y = l \cdot sin(\alpha)\] \[y` = l \cdot sin(\alpha + \theta)\] \[y` = l \cdot ( sin(\alpha)cos(\theta) + cos(\alpha)sin(\theta) )\] \[y` = y \cdot cos(\theta) + x \cdot sin(\theta)\]이를 행렬식으로 표현하면 다음과 같이 적을 수 있습니다.
\[x` = x \cdot cos(\theta) + y \cdot sin(\theta)\] \[y` = x \cdot sin(\theta) + y \cdot cos(\theta)\] \[\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \text{cos}\theta & -\text{sin}\theta \\ \text{sin}\theta & \text{cos}\theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\]좌표축 기준 회전 변환
2차원에서 회전 변환을 생각해봅니다. 2차원에서의 회전 변환은 z축을 기준으로 회전하는 것을 의미합니다.
이를 X축, Y축, Z축 각각에 대해서 회전 행렬을 구할 수 있스빈다.
- 각각의 축 기준 행렬들은 직교행렬이라고 할 수 있습니다. 직교행렬의 특징은, 두 직교 행렬을 곱하면, 그 결과 행렬도 반드시 직교 행렬이 된다는 것입니다.
임의의 축 기준 회전
임의의 축 \(w\)를 방향으로 하는 평면이 있을 때, 이 평면에서의 벡터 \(v\)의 회전을 생각합니다.
임의의 벡터 \(v\)에서 앞 방향, \(w\)를 윗 방향 이라고 생각하면, 오른쪽 방향 \(\hat{Right}\)을 구할 수 있습니다.
회전이 적용된 벡터 \(R_a(v_{perp})\)는 앞 방향에서의 벡터 \(r_1\) 그리고 오른쪽 방향의 벡터 \(r_2\)인 두 벡터의 합으로 표현할 수 있습니다.
\[R_a(v_{perp}) = r_1 + r_2\] \[r_1 = ||r_1|| \cdot \hat{Forward}\] \[r_2 = ||r_2|| \cdot \hat{Right}\]\(r_1\)는 \(cos\theta\)를 곱함으로 쉽게 구할 수 있습니다.
\[||r_1|| = cos \alpha \cdot ||v||\]\(r_1\)은 \(v\)와 같은 방향입니다. 따라서 \(r_1\)은 다음과 같이 쓸 수 있습니다.
\[r_1 = cos \alpha \cdot v\]회전 행렬을 만들어야 하므로 회전된 벡터의 길이는 동일해야 합니다. 회전된 벡터에서 \(r_2\)의 길이를 구하면 다음과 같이 쓸 수 있습니다.
\[||r_2|| = cos(90 - \alpha) \cdot ||v||\]\(cos(90-\alpha)\)는 \(sin(\alpha)\)로 쓸 수 있으므로,
\[||r_2|| = sin\alpha \cdot ||v||\]로 쓸 수 있습니다.
\[r_2 = sin\alpha \cdot ||v|| \cdot \hat{right}\]- 왼손 좌표계 기준
로드리게스 회전 공식
로드리게스 회전 공식(Rodrigues rotation formula)
임의의 벡터 \(a\)를 기준으로 각 \(α\)만큼 벡터 \(v\)를 회전시킨다고 하고, 이 회전변환을 \(R_a\)라고 한다면, 이때 벡터 \(v\)자신을 벡터 \(\)에 투영시킨 벡터 \(v_{proj}\)와 이 \(v_{proj}\)를 \(v\)로부터 빼서 나오는 \(v_{perp}\)를 구할 수 있습니다. 이는 마치 벡터 \(v\)를 서로 수직인 두 벡터 \(v_{proj}\)와 \(v_{perp}\)의 합으로 표현하는 것과 같습니다.

- \(\hat{a}\)는 벡터 \(a\)를 정규화한 벡터를 의미합니다.
- \(v_{proj}\)은 회전축인 벡터 \(a\)와 바향이 같으므로 회전에 아무런 영향을 받지 않습니다.
이 변환의 결과인 벡터 \(R_a(v)\)는 \(v_{perp}\)를 벡터 \(a\)를 기준으로 \(α\)만큼 회전시킨 벡터 R_a(v_{perp})와 \(v_{proj}\)의 합으로 나타낼 수 있습니다.
\[R_a(v) = v_{proj} + R_a(v_{perp})\]
벡터 \(v\)와 벡터 \(a\)에 대해 수직인 축 \(w\)를 생각합니다.
\[w = \hat{a} \times v\]
임의의 축을 기준으로 회전시키는 것을 생각하면 \(r_1\)을 구합니다.
\[||r_1|| = cos \alpha \cdot || r_a(v_{perp}) || = cos \alpha \cdot || v_{perp} ||\] \[r_1 = ||r_1|| \cdot \hat{v}_{perp}\] \[r_1 = \cos \alpha \cdot v_{perp}\]임의의 수직인 벡터, 벡터 \(a\)와 벡터 \(v\)의 사이각을 \(\theta\)라고 한다면, \(w\)는 \(v_{perp}\)와의 관계를 다음과 같이 적을 수 있습니다.
\[||w|| = sin \theta \cdot || \hat{a} || \cdot || v ||\] \[||w|| = sin \theta \cdot ||v||\] \[||w|| = || v_{perp} ||\]임의의 수직축 \(w\)는 회전하는 평면에서 \(\hat{right}\)의 방향으로 사용할 수 있습니다.
- 첫번째 그림에서 벡터 \(w\)를 그린 후 이동시키면 알 수 있습니다.
이제 \(R_a(v)\)를 구합니다.
\[R_a(v) = v_{proj} + R_a(v_{perp})\] \[R_a(v) = v_{proj} + cos\alpha \cdot v_{perp} + sin \alpha \cdot w\] \[R_a(v) = v_{proj} + cos\alpha \cdot (v - v_{proj}) + sin \alpha \cdot (\hat{a} \times v)\] \[R_a(v) = (v \cdot \hat{a}) \cdot \hat{a} + cos\alpha \cdot (v - (v \cdot \hat{a}) \cdot \hat{a}) + sin \alpha \cdot (\hat{a} \times v)\] \[R_a(v) = cos\alpha \cdot v + (1-cos\alpha) \cdot (v\cdot \hat{a}) \cdot \hat{a} + sin\alpha(\hat{a} \times v)\]이를 3차원 공간의 기저 벡터 \(i, j, k\)에 차례로 적용한 후 결과 벡터들을 열벡터들로 가지는 확장 행렬로 구성하여 \(R_a\)변환 행렬을 구합니다.
\[a = (a_x, a_y, a_z)\] \[c = \cos\alpha\] \[s = \sin\alpha\]기저 벡터 \(i, j, k\)에 차례로 적용한 후 결과 벡터들을 열벡터들로 가지는 확장 행렬을 구성하면 바로 \(R_a\)변환 행렬을 구할 수 있습니다.
- 주 대각성분에 \(\cos\alpha\)가 적용됩니다.
- 벡터와 행렬의 관계에서, \(\sin\alpha\)를 주대각성분을 제외한 부분에 추가할 수 있습니다.
- \((1-\cos\alpha)\cdot(v\cdot\hat{a})\cdot\hat{a}\)은 각 성분을 직접 곱해서 확장 행렬을 구할 수 있습니다.
- 첫번 째 내적에서 주 대각성분에 \(\hat{a}\)가 적용됩니다. 그 다음 스칼라와 \(\hat{a}\)의 내적에서 \(v\)에 대해 모든 \(\hat{a}\)의 성분이 적용되므로, 행렬에 적용시킬 수 있습니다.
선형 변환 조합
어떤 벡터 \(v\)를 선형 변환 \(S\)와 \(T\)를 차례로 적용하여 벡터 \(w\)로 변환한다면 다음과 같이 적을 수 있습니다.
\[w = T(S(v))\]두 선형 변환을 연속적으로 적용하는 것 역시 하나의 선형 변환입니다.
\[F(x) = T(S(x))\]\(F(x)\)는 선형변환의 두 특성이 성립하니다.
\[F(v+w) = T(S(v+w)) = T(S(v)+S(w)) = T(S(v)) + T(S(w)) = F(v)+F(w)\] \[F(a \cdot v) = T(S(a \cdot v)) = T(a \cdot S(v)) = a \cdot (T(Sv))s = a \cdot F(v)\]- 선형 변환을 행렬로 나타내기 위해서는 각각의 기저 벡터들에 선형 변환을 적용하고 그 결과로 나온 열벡터들로 확대 행렬을 만들면 됩니다.
선형 변환 조합의 행렬 곱셉
선형 조합된 선형 변환을 풀면 이는 행렬 곱셉과 같다는 것을 알 수 있습니다.
- 선형 변환이 적용되는 순서와 행렬 곱셉의 순서는 반대여야 합니다.
게임에서 선형 변환들의 조합을 행렬 곱셉을 통해서 하나의 행렬로 표현하는 이유는, 3D 게임에서는 같은 선형 변환들의 조합을 여러 번 적용하는 경우가 많습니다. 이때, 두 변환행렬을 하나의 행렬로 만들고 이를 재사용 하면, 두 변환을 각각 적용시키는 것보다 연산의 양이 반으로 줄어들 수 있습니다.
- 선형 변환들이 많을 수록 그 효과는 매우 클 것 입니다.
Affine Space
프랑스 수학자 버거(Marcel Berger)는 ‘아핀 공간이란 벡터 공간의 선형 대응에 이동을 추가하여, 우리가 벡터 공간의 중심을 잊으려고 하는 것에 불과하다’
수학으로 시작하는 3D 게임 개발의 필자의 생각은 `아핀 공간에서는 기저 벡터와 상관없이 두 점의 뺄셈으로 한 벡터를 표현할 수 있고 그들의 모임은 벡터 공간을 이루므로, 따라서 아핀 공간에서는 원점을 어디로 정하든 그것을 구성하는 점들로부터 벡터 공간을 만들어 낼 수 있고 그래서 벡터 공간의 중심을 잊을 수 있습니다.
기하학에서 아핀 공간은 유클리드 공간의 아핀 기하학적 성질들을 일반화해서 만들어지는 구조입니다. 아핀 공간에서는 점에서 점을 빼서 벡터를 얻거나 점에 벡터를 더해 다른 점을 얻을 수는 있지만 원점이 없으므로 점과 점을 더할 수는 없습니다.

- 게임에서 캐릭터들의 위치는 점으로 표현합니다.
점(Point)과 벡터(Vector)
직교 좌표계에서 점은 원점으로부터 각 축을 따라 얼마만큼 떨어져 있는지로 표현됩니다.
3차원 공간에서 한 점 P가 원점으로부터 \(x, y, z\)축을 따라 각각 \(p_x, p_y, p_z\)만큼 떨어져 있을 때 다음과 같이 표현됩니다.
\[P = (p_x, p_y, p_z)\]\(V\)라는 벡터 공간이 있을 때, 이 V위에 아핀 공간은 \(A\)라는 점들의 집합으로 정의됩니다. 이떄 \(V\)와 \(A\)사이에 아래와 같은 두 대응(map)이 존재하고 다음 세 가지 성질을 만족합니다.
\[A \times V \rightarrow\] \[P,v | \rightarrowtail P + v\]- \(A\)에 속한 모든 점 \(P\)에 대해서 \(P+\overrightarrow{0}=P\)입니다. 영 벡터(\(\overrightarrow{0}\))는 벡터 공간 V의 항등원입니다.
- \(A\)에 속한 모든 점 \(P\)와 \(V\)에 속한 임의의 벡터 \(v,w\)에 대해 \(P+(v+w)=(P+v)+w\)가 성립합니다.
- \(A\)에 속한 점 \(P,Q\)가 있을 때 \(P+v=Q\)를 만족하는 단 하나의 벡터 \(v\)가 존재합니다.
아핀 공간의 정의에 대해서 첫 번째 대응이 말하는 것은, 아핀 공간에서 점과 벡터를 가지고 어떤 연산을 하면 그 결과가 점이 된다는 것을 의미합니다.
두 번째 대응은 첫 번째 대응이 어떤 연산을 점과 벡터의 덧셈 연산이라고 정의한 후 출발합니다. 이 때 어떤 점과 벡터의 짝(P,v)는 그들의 덧셈 연산 (P+v)과 일대일 대응(\(bijection, \rightarrowtail\)) 관계를 이룬다는 뜻 입니다.
쉽게 말해서 한점과 한 벡터의 짝은 오직 단 하나의 덧셈 연산으로만 대응되며, 이 덧셈 연산은 다시 그 둘의 짝으로만 대응 된다는 말입니다.
이 두 대응관계가 있고 위의 세 조건을 만족해야지만 비로소 아핀 공간이 정의됩니다.
3차원 공간에서 점과 벡터의 덧셈 연산은 다음과 같이 정의합니다. P와 Q가 점이고 v가 벡터일 때 P와 v의 덧셈은 다음과 같습니다.
\[P = (p_x, p_y, p_z)\] \[v = (v_x, v_y, v_z)\] \[Q = P + v\] \[Q = (p_x, p_y, p_z) + (v_x, v_y, v_z)\] \[Q = (p_x + v_x, p_y + v_y, p_z + v_z)\]3차원 공간에서 점과 벡터는 같은 방식으로 표현되고 벡터와 벡터를 더하거나 점과 벡터를 더하거나 계산하는 방식 역시 동일합니다. 따라서 아핀 공간에서 덧셈 연산을 수식화할 때는 이것이 벡터와 벡터의 덧셈인지 점과 벡터의 덧셈인지 정확히 말해주어야 합니다.
위의 두 가지 성질은 다음과 같이 정의할 수 있습니다.
\[P + \overrightarrow{0} = (p_x+0, p_y+0,p_z+0)\] \[P + \overrightarrow{0} = (p_x, p_y, p_z)\] \[P+(v+w) = P+(v_x + w_x, v_y + w_y, v_z + w_z)\] \[P+(v+w) = (p_x + v_x + w_x, ...)\] \[(P+v)+w = (p_x + v_x, p_y + v_y, p_z + v_z) + w\] \[(p+v)+w = (p_x + v_x + w_x, ...)\]세 번째 조건은 기하학적으로 보면 P에 어떤 벡터를 더해서 Q로 만들고자 할 때 그 벡터는 v이외의 어떤 것도 될 수 없음이 자명합니다.
다른 점으로 향하는 벡터를 구하고자 한다면 끝점에서 시작점을 빼는 연산으로 그 벡터를 구할 수 있습니다.
- 벡터 ± 벡터 = 벡터
- 점 ± 벡터 = 점
- 점 - 점 = 벡터
선
아핀 기하학적 현상(geometric shapes)중에 하나인 선(line)을 봅니다.
3차원 공간에서 두 점을 이용해서 선을 다음과 같이 정의할 수 있습니다.
\[v = Q - P\] \[L(t) P + t \cdot v\]- t 값은 음의 무한대부터 양의 무한대 사이의 실수들입니다.
점 P에다가 벡터 v의 크기를 마음대로 조정하여 더하면 그 결과 점들이 벡터 v와 같은 방향을 가진 직선을 이룬다는 것을 쉽게 이해할 수 있습니다.
- 아핀 조합에 참여한 점들은 서로 아핀 독립(affinely independent)입니다. 선형 독립이 임의의 한 기저 벡터가 나머지 기저 벡터들의 선형 조합으로 만들어질 수 없음을 의미하듯, 아핀 독립 역시 비슷하게 점 집합에서 임의의 한 점이 나머지 점들의 아핀 조합으로는 만들어질 수 없다는 것을 말합니다.
간단하게 두 점으로 표현한다면
간단하게 두 점만으로도 표현 할 수 있습니다.
\[L(t) = (1-t) \cdot P + t \cdot Q\]t가 0, 1이라면 점 P가, 점 Q가 됩니다.
점 P와 Q를 합성하여 좌표를 만들 때, t 0.5라고 하면 점 P를 0.5 만큼 곱한 값과 점 Q를 0.5만큼 곱한 값으로 위치하게 됩니다. 즉 점 P와 점 Q의 가운데에 위치하게 됩니다.
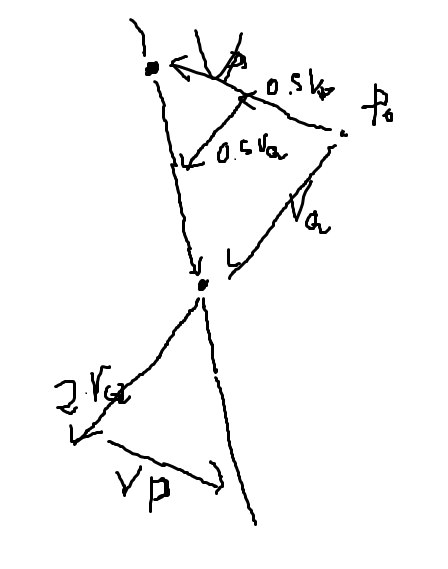
각 기저벡터들에서 곱해지는 스칼라 값들의 합은 반드시 1
\(v_1,v_2,...v_n\)벡터들을 \(P_0\)이 중심인 \(n\)차원 벡터 공간의 기저 벡터라고 하면 벡터 \(v\)는 기저 어떤 점 \(P_i\)에서 원점 \(P_0\)를 빼는 것으로 나타낼 수 있습니다.
\[v_1 = P_1 - P_0\] \[v_2 = P_2 - P_0\] \[...\] \[v_2 = P_2 - P_0\]이를 다음과 같은 수식으로 나타내면
\[P = P_0 + (a_1 \cdot v_1 + ... + a_n \cdot v_n)\] \[P = P_0 + a_1 \cdot (P_1 - P_0) + ... + a_n \cdot (P_n - P_0)\]각 점들에 곱해지는 스칼라 값들의 합이 반드시 1임을 알 수 있습니다.
\[(1 - a_1 .. - a_n) + a_1 + ... + a_n = 1\]- 두 점으로 선을 표현을 보면 보다 쉽게 이해할 수 있습니다.
선분(line segment)
\(L(t) = (1-t)P + tQ\) \(0 ≤ t ≤ 1\)
로 표현할 수 있습니다.
반직선(ray)
\(L(t) = (1-t)P + tQ\) \(0 ≤ t\)
의 경우 0이상으로 표현 할 수 있습니다.
면(Plane)
면은 세 점의 아핀 조합을 통해서 생성된 2차원 아핀 공간이며 매개 변수 방정식을 통해서 표현할 수 있습니다.
평면상에 위치한 세 점 \(A,B,C\)가 있을 때, 이 면은 다음과 같이 매개변수 방정식 \(P\)로 나타낼 수 있습니다.
\[P(s,t) = (1-s-t) \cdot A + s \cdot B + t \cdot C\] \[P(s,t) = A + s \cdot (B - A) + t \cdot (C - A)\] \[P(s,t) = A + s \cdot u + t \cdot v\]길이가 마음대로 조정 가능한 두 벡터를 한점에 더해서 하나의 평면이 생성되는 것을 머리속에 그릴 수 있습니다.
평면을 일반화 방정식으로 나타내면 다음과 같습니다.
- 3D 게임에서 평면은 일반화 방정식을 통해 나타냅니다.
점 \(P\)에서 평면상의 임의의 점 \(Q\)로 향하는 벡터를 \(v\)라고 하면 벡터 \(v\)는 평면의 방향 \(n\)과 수직이여야 합니다. 따라서 다음과 같이 나타낼 수 있습니다.
\[Q = (x, y, z)\] \[v = Q - P\] \[n \cdot v = 0\] \[n \cdot (Q - P) = 0\] \[n \cdot Q - n \cdot P = 0\] \[a \cdot x + b \cdot y + c \cdot z - n \cdot P = 0\]여기서 \(d=-n \cdot P\)라고 하면 위의 수식은 다음과 같이 쓸 수 있습니다.
\[ax + by + cz + d = 0\]이를 평면의 일반화 방정식이라 하며, 평면에 수직인 벡터 \(n\)은 평면의 법선 벡터(normal vector)라고 불립니다.
-
대개 정규 벡터로 평면의 방정식으로 이용합니다.
-
세 점으로 평면을 만들 때, 벡터를 곱하는 순서에 따라 평면은 바뀌지 않지만 법선 벡터의 방향이 바뀌게 됩니다.
임의의 점 P와 평면의 관계
임의의 점 \(P = (p_x,p_y,p_z)\)와 평면 \(ax+by+cz+d=0\)이 있을 때, 법선 벡터 \(n=(a,b,c)\)가 단위 벡터라면,
\(ap_x+bp_y+cp_z+d=k\)일 때 |k|는 점 \(P\)와 이 평면 사이의 거리입니다.
\[n \cdot ( P - P_{Origin} ) = k\] \[\|1\| \| ( P - P_{Origin} ) \| \cdot \cos \alpha = k\]이는 평면의 원점에서 점 \(P\)로 가는 벡터를 법선 벡터 \(n\)에서 투영했을 때, 길이를 나타나게 됩니다.
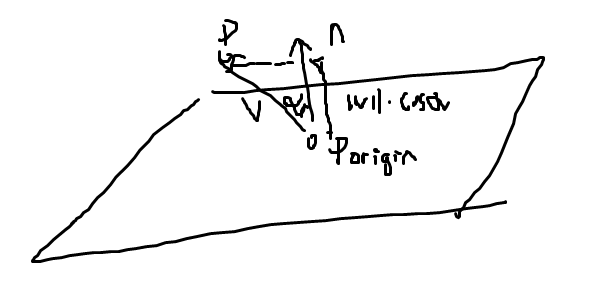
따라서 위의 관계를 보면
임의의 점 \(P = (P_x, P_y, P_z)\)와 평면 \(ax+by+cz+d=0\)이 있다고 했을 때, \(aP_x+bP_y+cP_z+d=k\)일 때, 만약 \(k>0\)이면 \(P\)는 평면 앞에 있고, \(k<0\)이면 \(P\)는 평면 뒤에 있습니다. \(k=0\)이면 당연히 \(P\)는 평면 위에 있습니다.
평면상의 점(coplanar points) 구하기
어떤 네 점 \(A,B,C,D\)가 같은 평면에 있는지 알기 위해서는
\[u = B - A\] \[v = C - A\] \[w = D - A\]\(u \cdot ( v \times w ) = 0\)이면 네점 A,B,C,D는 동일 평면상의 점들임을 알 수 있습니다.
삼각형 (Triangle)
- 개발자들 사이에서 흔히 폴리곤(polygon)이라고 불리지만 사실 정확히 폴리곤은 삼각형이 아닌 다각형을 의미합니다.
3D 게임에 등장하는 물체들은 점들의 집합입니다. 하지만 아무리 많은 점을 사용해도 현실에 존재하는 물체들과 완전히 똑같이 표현하는 것은 사실상 불가능합니다. 따라서 어느 정도의 정밀도로 타협을 해서 물체를 이루는 점의 개수가 정해집니다. 이 점들을 차례로 이어서 선들을 이루고 선들은 다시 삼각형을 구성하며 각각의 삼각형 영역에 적당한 색들을 채우고 나면 비로소 3차원 모델이 그려지는 것입니다.
삼각형 안에 점이 위치하는지
세 점 \(A,B,C\)로 이루어진 삼각형이 있고 점 \(D\)가 있다고 하면, 이들로부터 다음 여섯 개의 벡터를 정의할 수 있습니다.
\[u_1 = D - A\] \[u_2 = D - B\] \[u_3 = D - C\] \[v_1 = B - A\] \[v_2 = C - B\] \[v_3 = A - C\]이를 이용해 다음 세 벡터를 만들 수 있습니다.
\[w_1 = u_1 \times v_1\] \[w_2 = u_2 \times v_2\] \[w_3 = u_3 \times v_3\]점 D가 삼각형의 안에 있다면 위의 세 벡터 \(w_1,w_2,w_3\)의 방향은 모두 같아야 합니다. 점 \(D\)가 삼각형 내부에 있다면, 벡터 \(u_i\)에서 벡터 \(v_i\)로의 방향이 항상 시계 방향임을 알 수 있습니다.
따라서 점 \(D\)가 삼각형 \(ABC\)안에 있다면 다음이 성립합니다.
\[w_1 \cdot w_2 > 0\] \[w_2 \cdot w_3 > 0\] \[w_3 \cdot w_1 > 0\]더 빠르게 삼각형 안에 점이 위치하는지
더 빠르게 해결하는 다른 방법은 면의 매개변수 방정식, 즉 아핀 조합을 이용하는 방법입니다.
\[P(s,t) = (1-s-t) \cdot A + s \cdot B + t \cdot C\] \[P(s,t) = A + s \cdot (B - A) + t \cdot (C-A)\] \[P(s,t) = A + s \cdot u + t \cdot v\]점 A에서 벡터로 삼각형을 그린 다면, \(s, t\) \(s+t\)의 범위로 삼각형에 있는지 알 수 있습니다.
점 A에서 D로 가는 벡터는 다음과 같이 표시할 수 있습니다.
\[D - A = w = s \cdot u + t \cdot v\]미지수 \(s\)와 \(t\)를 구하기 위해서는 두 개의 방정식이 필요합니다. 이를 위해 식에 각각 \(u\)와 \(v\)를 양변에 내적하여 두 방정식을 만들 수 있습니다.
\[w \cdot u = (s \cdot u + t \cdot v) \cdot u\] \[w \cdot u = s \cdot (u \cdot u) + t \cdot (v \cdot u)\] \[w \cdot v = (s \cdot u + t \cdot v) \cdot v\] \[w \cdot v = s \cdot (u \cdot v) + t \cdot (v \cdot v)\]\(w, u, v\)를 알고 있으므로, 두 연립방정식을 풀면 다음과 같이 구할 수 있습니다.
\[s = \frac {(v \cdot v) \cdot (w \cdot u) - (v \cdot u)\cdot(w \cdot v)} {(u \cdot u) \cdot (v \cdot v) - (u \cdot v)\cdot(v \cdot u)}\] \[t = \frac {(u \cdot u)\cdot(w \cdot v) - (u \cdot v)\cdot(w \cdot u)} {(u \cdot u)\cdot(v \cdot v) - (u \cdot v)\cdot(v \cdot u)}\]-
위 식은, 두 벡터를 이용해서, 해당 점으로 가는 값을 벡터를 만들기 위해 합성 비를 구하는 것으로 이해할 수 있습니다.
-
위 식은 \(D=A+(s \cdot u + t \cdot v)\)방정식을 풀은 식이기 때문에 평면 위에 없다면 성립하지 않습니다.
Affine Transformation (아핀 변환)
기하학에서 아핀 변환은 아핀 기하학적 성질들을 보존하는 두 아핀 공간 사이의 함수이다.
더 일반적으로, 아핀 변환 은 아핀 공간 (유클리드 공간은 특정 아핀 공간임)의 자동형성입니다. 즉, 아핀 하위 공간 의 차원 을 모두 유지하면서 아핀 공간을 자신에게 매핑 하는 함수 입니다 (즉, 점, 선 대 선, 평면 대 평면 등) 및 평행 선분의 길이 비율. 결과적으로, 병렬 아핀 부분공간 세트는 아핀 변환 후에 평행을 유지합니다.아핀 변환은 직선 위에 있는 점 사이의 거리 비율을 유지하지만 선 사이의 각도나 점 사이의 거리를 반드시 보존하지는 않습니다.
그 외

아핀 자기 유사성 을 나타내는 양치류 와 같은 프랙탈 ( Barnsley’s fern )의 이미지 . 양치류의 각 잎은 아핀 변환에 의해 서로 관련이 있습니다. 예를 들어, 붉은 잎은 반사, 회전, 크기 조정 및 변환을 조합하여 진한 파란색 잎과 연한 파란색 잎으로 변환할 수 있습니다.
선형 변환의 순서
선형 변환을 적용할 때 적용 순서에 따라 다른 결과를 가져올 수 있습니다.

원점에서 각 점으로 향하는 8개의 벡터 (큐브 모델)이 있다고 합니다.

2배로 늘리는 크기 변환의 표현입니다.

원점이 아닐 때 크기변환을 적용한 결과입니다.

회전 변환을 적용한 결과입니다.

원점이 아닐 때 회전변환을 적용하면 다음의 결과입니다.
- 회전 변환의 적용 순서는 Scale, Rotation, Translation입니다.
- 선형 변환을 행렬 식으로 표현하면 역순으로 곱해야 하므로 \(P^` = T \cdot R \cdot S \cdot P\)가 됩니다.
위치 변환
위치 변환은 선형 변환이 아닙니다. 행렬의 곱셈으로 표현할 수가 없어서 차원을 하나 늘려, 담아서 사용합니다.
한차원 늘리지 않고 위치 변환을 추가하면 다음과 같습니다.
\[P^{`} = M \cdot P + A\]이에 선형변환을 계속 적용하면 심각하게 복잡해 집니다.
\[P^{``} = N \cdot P` + B = N \cdot ( M \cdot P + A) + B = N \cdot M \cdot P + N \cdot A + B\] \[P^{```} = Q \cdot N \cdot P + Q \cdot N \cdot A + Q \cdot B + C\]이 식을 다음과 같이 표현하기 위해서 한 차원을 확장 합니다.
\[P^{`} = M \cdot P\] \[P^{``} = N \cdot M \cdot P\] \[P^{```} = Q \cdot N \cdot M \cdot P\]2차원 위치 변환을 3차원으로 표현





이렇게 만들어진 변환을 3차원 공간의 선형 변환 중 밀기 변환(shearing)이라고 합니다.
이 조차도 2차원으로 줄여서 생각하면,
\[x^{`} = x + m \cdot y\] \[y^{`} = y\]로, x 성분 값을 y성분에 비례 게수 m을 곱한 것을 더해서 변환하는 것을 말합니다.


한 차원 확대해서 위치 변환을 표현하면 다음과 같습니다.
\[\begin{bmatrix} 1 & 0 & 0 & a \\ 0 & 1 & 0 & b \\ 0 & 0 & 1 & c \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} = \begin{bmatrix} P_x + a \\ P_y + b \\ P_z + c \\ 1 \end{bmatrix}\]Homogeneous Coordinates (동차 좌표계)
위의 차원의 확장에서 마지막 성분에 1을 추가하여 차원을 확장하는 것은 동차 좌표계라는 개념을 바탕으로 합니다.
어떤 목적을 위해 한 차원의 좌표(n) 을 추가한 좌표 (n+1)로 표현을 하는 것을 동차 좌표계라고 합니다. 시점으로 보이는 점들의 위치가 중요한 것이 아니라 시점으로 부터의 방향이 중요하기 때문에 동차좌표를 사용합니다.
- 사영기하학에서 동차좌표는 n차원 사영 공간을 n+1개의 좌표로 나타내는 좌표계입니다.
수학 에서 아우구스트 페르디난트 뫼비우스( August Ferdinand Möbius )가 1827 년 저서 Der barycentrische Calcul 에서 소개한 동차 좌표 또는 투영 좌표는 데카르트 좌표 가 유클리드 기하학 에서 사용되는 것처럼 투영 기하학 에서 사용되는 좌표 시스템입니다.그들은 다음을 포함하는 점의 좌표가 있다는 이점이 있습니다.무한대의 점, 유한 좌표를 사용하여 나타낼 수 있습니다. 동차 좌표를 포함하는 공식은 데카르트 좌표보다 더 간단하고 대칭적인 경우가 많습니다. 동차 좌표는 컴퓨터 그래픽 및 3D 컴퓨터 비전 을 포함하여 다양한 응용 프로그램을 가지고 있으며, 여기서 아핀 변환 및 일반적으로 투영 변환 을 행렬 로 쉽게 표현할 수 있습니다.
- 투영 변환은 실세계 3차원 좌표 한점을 2차원으로 변환하는 것을 말합니다.
- 동차좌표계는 차원의 좌표를 1차원 증가시켜 표현하는 방법을 동차좌표계라고 합니다.

무한 원점
3차원 좌표 \((x, y, z)\) 3가지 성분에 무한 원점이라는 개념을 추가하면 \((x, y, z, w)\)로 표현할 수 있습니다.
\[(x, y, z) \rightarrow (w \cdot x, w \cdot y, w), w ≠ 0\]가장 간단한 형태는 w가 1인 경우로 직교 좌표계 점의 성분을 그대로 가지고 마지막 성분으로 1을 추가한 것입니다.
- 무한원점의 개념이 어려우만 4차원의 성분이 0이면 벡터, 1이면 점이라고 생각합니다.
거꾸로 동차 좌표계 점은 아래와 같이 직교 좌표계 점으로 대응시킬 수 있습니다.
\[(x, y, z, w) \rightarrow (x / w, y / w, z / w)\]- 참고로 동차 좌표계가 직교 좌표계와 혼동되는 것을 피하고자 \((x:y:w)\) 혹은 \([x:y:w]\)와 같은 방식으로 사용한다고 합니다.
투영 공간에 적용되는 선형 변환
직교 평면에 적용되는 선형 변환이 있듯이 투영 공간에 적용되는 선형변환도 있습니다. 이를 투영 변환(projective transformation)이라고 합니다.
- 이때 투영 변환 행렬의 요소 중 g와 h가 모두 0이고 k가 0이 아니라면, 이 변환은 해당 동차 좌표계에 대응하는 직교 좌표계의 아핀 변환가 같습니다.
1에 따라 동차 좌표계에 대응하는 선형 변환들을 계산해볼 수 있습니다.
선과 면의 아핀 변환
선의 아핀변환인 경우 다음 중에서 선택할 수 있습니다.
\[P^` = M \cdot P\] \[Q^` = M \cdot Q\] \[v^` = Q^` - P^`\] \[v^` = M \cdot v\] \[L^`(t) = P^` + t \cdot v^`\]면의 경우를 생각해 보면 다음과 같습니다.
- 처음 주어진 성분들을 변환하면, \(M \cdot n\), \(M \cdot P\)로 생각할 수 있습니다.
평면의 방정식을 \(K, P\)로 나타내면 다음과 같습니다.
\[K = (a, b, c, d)\] \[P = (p_x, p_y, p_z, 1)\] \[K^T \cdot P = \begin{bmatrix} a & b & c & d \end{bmatrix} \cdot \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} = \begin{bmatrix} a \cdot P_x + b \cdot P_y + c \cdot P_z + d \end{bmatrix} = 0\]점 P와 K를 변환한 후에 각각 \(P^`, K^`\)라고 한다면 이들도 당연히 평면 방정식을 만족하기 때문에 다음과 같은 식은 항상 참이어야 합니다.
\[K^{`T}\cdot P^` = 0\]\(P\)의 경우 아핀 변환 행렬 \(M\)을, \(K^`\)의 경우 아핀 변환 행렬 Q를 적용했다고 하면 다음과 같습니다.
\[(Q \cdot K)^T \cdot M \cdot P = 0\] \[K^T \cdot Q^T \cdot M \cdot P = 0\]위의 식을 \(K^{T}\cdot P = 0\)가 성립하게 만드는 조건은 다음과 같습니다.
\[Q^T \cdot M = I\]따라서 \(Q\)는 다음과 같이 쓸 수 있습니다.
\[Q^T = M^{-1}\]주요 참고자료 : 수학으로 시작하는 3D 게임 개발, 위키피디아
